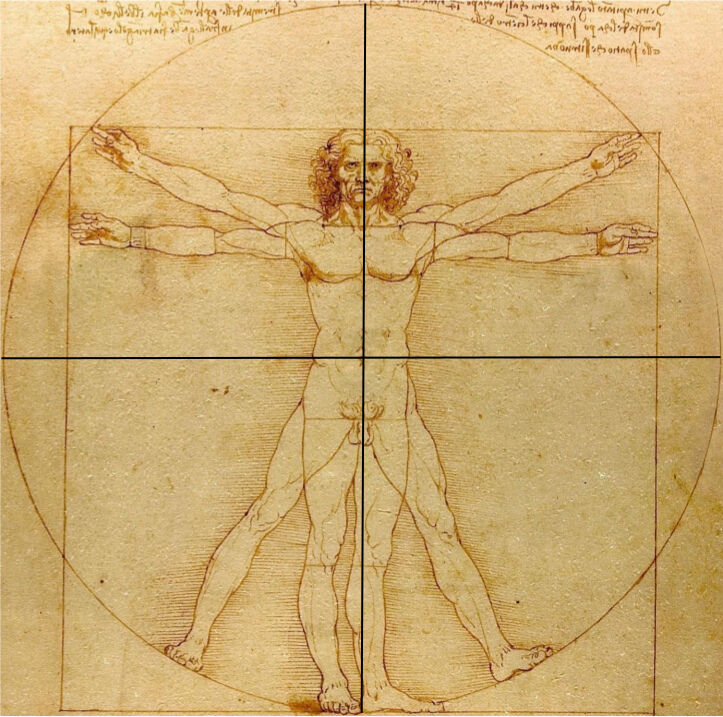
Comprends bien !
Du Un fais Dix
Et laisse Deux tranquille
Et fais pareil pour Trois
Te voilà riche !
Perds le Quatre
De Cinq et Six,
La sorcière le dit,
Fais Sept et Huit.
Ainsi c’est accompli !
Et Neuf est Un
Et Dix n’est rien
C’est là le « Une fois Un » de la sorcière.
— Goethe, Faust
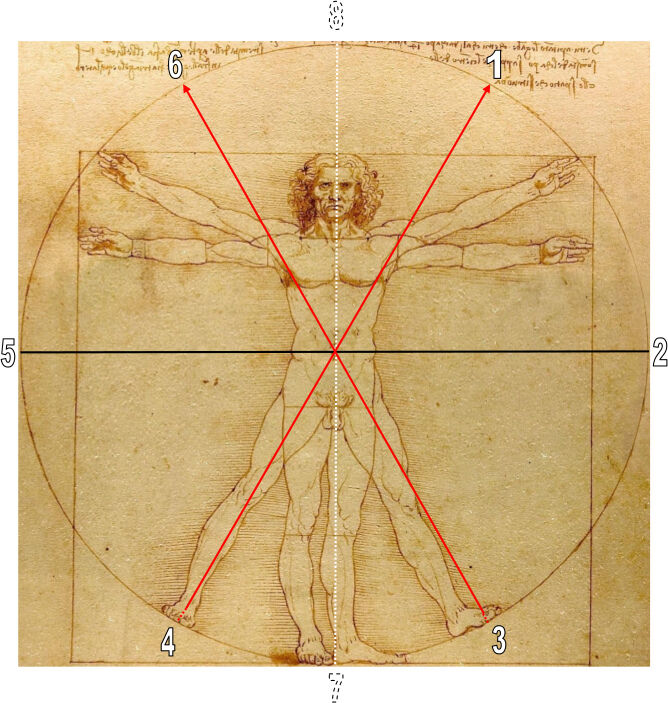
Dans la figure qui précède, nous avons placé les six directions – telles que l’étude des kajo nous a amené à les définir – dans le cercle de l’homme de Vitruve, pour voir si nous pourrions – grâce aux proportions du corps humain – obtenir une confirmation de la voie que nous avons balisée dans cette étude.
Dans les kajo, nous avons divisé le cercle selon l’angle de 60° qui définit 6 secteurs égaux (6x60°=360°), et non pas selon l’angle de 45° qui définit 8 secteurs égaux (8x45°=360°). La raison de ce choix, c’est que nous faisons confiance à O Sensei et que nous sommes donc partis des explications de Budo, qui indiquent sans ambiguïté qu’il existe 6 directions possibles à partir de la position hanmi :
Faire face à l’adversaire avec une attitude d’Aiki hanmi irimi, en ouvrant les pieds dans les six directions (roppo).
— Morihei Ueshiba, Budo, Edition originale japonaise, 1938.
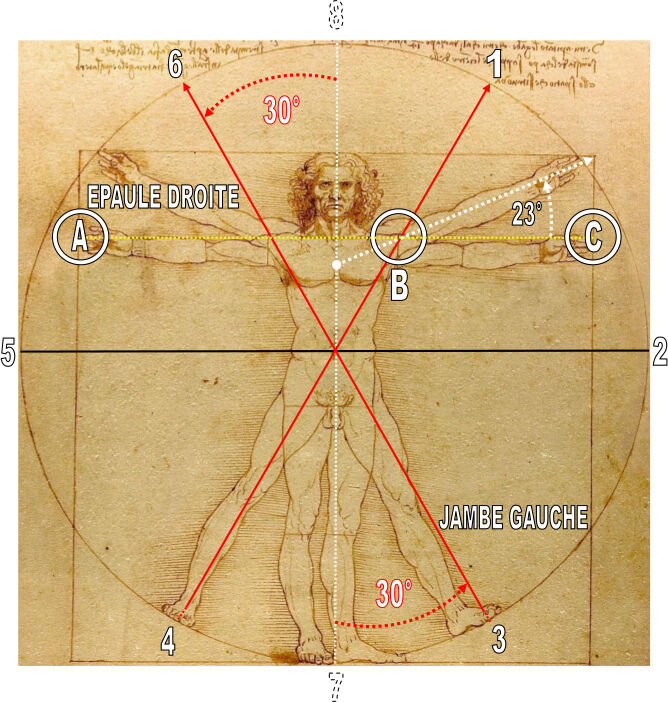
La première surprise vient cette fois encore des pieds de l’homme de Vitruve. En effet, les deux diamètres rouges, à 30° chacun d’inclinaison par rapport à l’axe vertical, prennent leur origine exactement au centre de chacun des pieds écartés, et plus précisément encore au centre de la balle du pied, qui est la zone d’appui du pratiquant d’Aikido en mouvement (le talon doit toujours rester léger dans les déplacements). L’écartement des pieds de l’homme de Vitruve aux points d’appui est donc très exactement de 60°.
Remontons le long de ces axes.
Notre deuxième surprise est de voir qu’ils coupent l’articulation des épaules avec une précision parfaite. Comme si l’angle de 60° des pieds écartés pointait sur l’articulation des épaules. Mais peut-être ne s’agit-il là que d’une coïncidence, un effet du hasard.
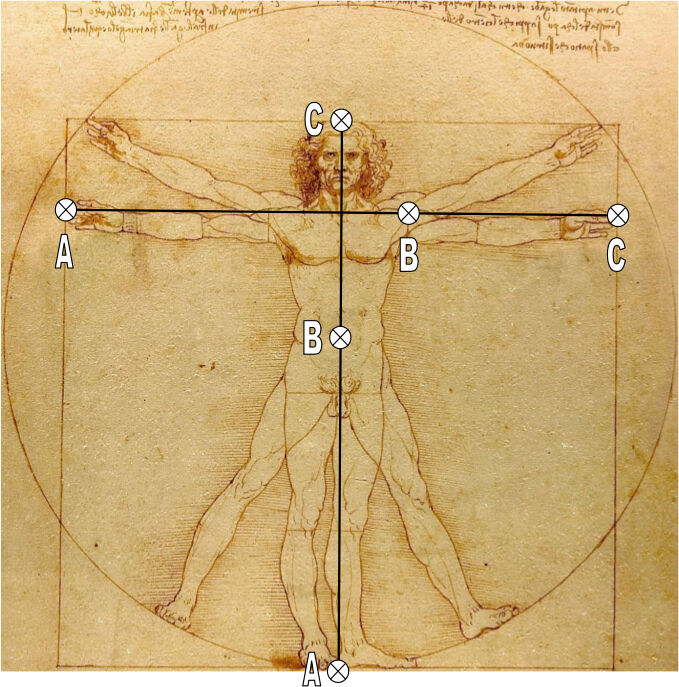
Il se trouve que Léonard de Vinci nous a donné un moyen d’en avoir le cœur net, il a laissé, à la base du cou, sur les clavicules, un trait de construction (vraisemblablement utilisé pour aligner la partie supérieure des bras) qu’il suffit de prolonger (en jaune sur la figure ci-dessous) pour vérifier qu’il coupe bien l’articulation des épaules au même point exactement que les diamètres rouges, et précisément sur le trait vertical de limite de l’épaule dessiné par Léonard.
Or ce point nous l’avons déjà rencontré et nous le connaissons bien :
1 - Nous savons, depuis HV #3, qu’il s’agit du point (B) qui partage la longueur des bras entre les deux côtés du carré (AC) en moyenne et extrême raison, c'est-à-dire selon le nombre d’or:
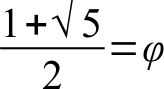
2 – Nous savons aussi, depuis HV #4, que ce point est en même temps le centre du cercle qui commande le rapport entre l’axe vertical du corps et le cercle circonscrit, par l’intermédiaire de l’unique angle possible, celui de 23°.
Reportons tout cela sur notre homme de Vitruve :
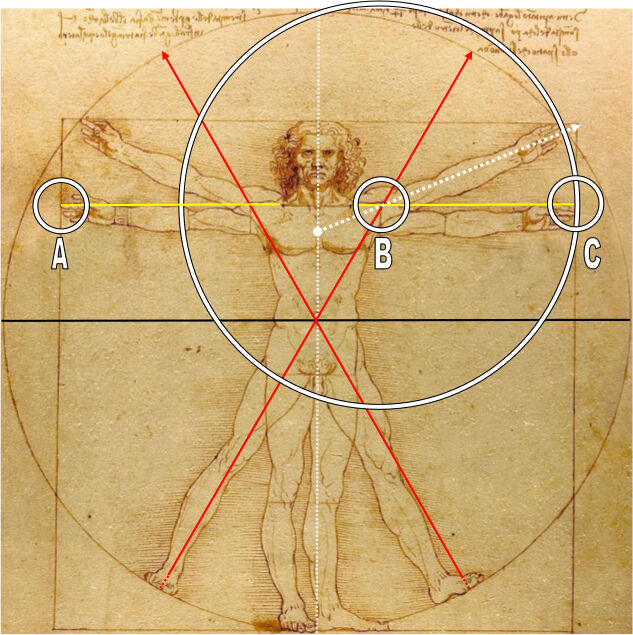
Il est très douteux que le hasard puisse mener à un arrangement aussi rigoureux que celui qui apparaît dans la construction de ce dessin.
On peut toujours invoquer qu’un faisceau de coïncidences n’est pas encore une preuve. Toutefois, ne serait-il pas très étonnant qu’il existe, en plus des trois coïncidences que nous avons déjà relevées, une quatrième plus remarquable encore que les trois premières ? Nous prenons ici le terme de coïncidence dans le sens de recouvrement exact de points ou de lignes qui est le sien en géométrie.
Voyons cela.
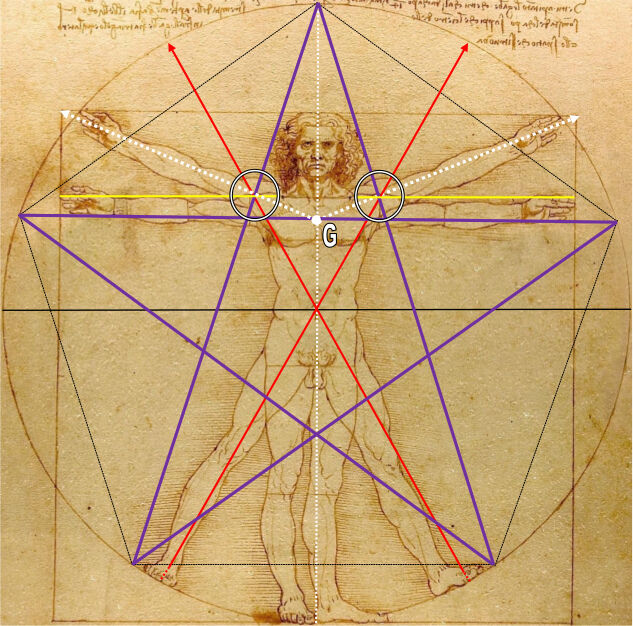
Puisque nous connaissons depuis HV #4 le pentagone régulier inscrit, utilisons-le pour dessiner maintenant la plus célèbre des figures géométriques, le pentacle, le pentagramme régulier inscrit dans le cercle, cette étoile flamboyante qui était le cœur de l’enseignement secret des Pythagoriciens, et leur signe de ralliement :
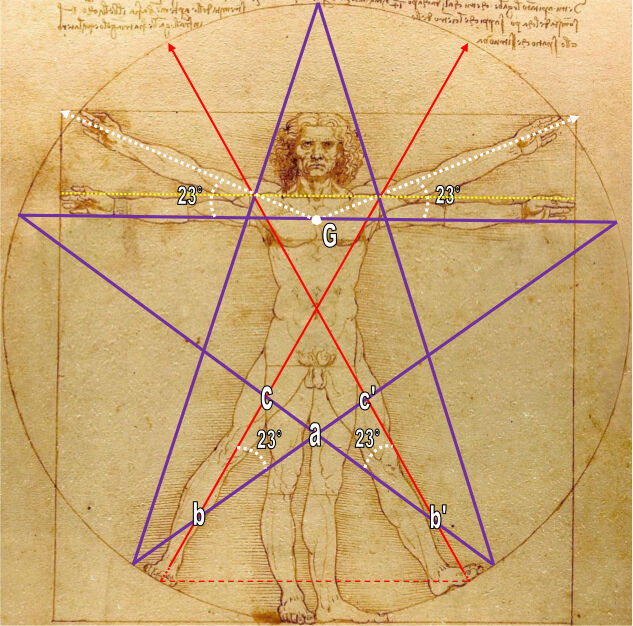
Les deux montants de la pointe de l’étoile flamboyante dirigée vers le Ciel coupent l’articulation des épaules au même point très exactement que les trois autres droites.
Le moins que l’on puisse dire, si l’analyse géométrique a un sens, c’est que l’articulation de l’épaule humaine est un point très particulier, et qu’il convient de la regarder avec beaucoup d’attention. Dans un tel contexte, la phrase du Fondateur :
La forme de la technique d’Aikido est un entraînement pour délier les articulations.
— Morihei Ueshiba, Takemusu Aiki, vol.I, p.155, Editions Cénacle de France
prend un sens qui n’est peut-être pas simplement physiologique.
Il n’est pas interdit de penser, dès lors, que les immobilisations de nikyo, sankyo et kote gaeshi aient peut- être une signification plus profonde que le simple « contrôle » d’uke auquel elles sont généralement réduites. Et ce d’autant plus que, sur le plan martial, se mettre à genoux pour immobiliser un adversaire est une folie suicidaire incompréhensible.
J’attire en outre l’attention des Aikidokas sur un fait qui doit absolument être pris en considération : toutes les techniques fondamentales de l’Aikido passent par une mobilisation de l’épaule (Ikkyo, nikyo, sankyo, yonkyo, gokyo, shiho nage, kote gaeshi, kaiten nage, tenchi nage, à l’exception notable d’irimi nage). On peut traduire cette réalité de la manière suivante :
C’est par l’intermédiaire de l’articulation de l’épaule – donc du rapport φ – que tori transmet son énergie au point G d’uke, accédant ainsi à l’axe de son corps.
Autrement dit, pour neuf techniques sur dix, à cause de la médiation systématique de ce point géométrique si particulier de l’articulation de l’épaule, le mouvement d’Aikido s’effectue selon le rapport:
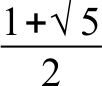
La seule technique qui puisse atteindre le point G d’uke sans passer par son épaule est une union directe des deux axes de tori et d’uke, une fusion de ces axes, c’est irimi nage.
Dans ce dernier cas, le mouvement d’Aikido s’effectue selon le rapport 1.
C’est pourquoi irimi nage occupe une place particulière parmi les techniques de l’Aikido, c’est elle qui exprime le mieux l’unité... parce qu’elle est l’unité.
Notons bien ceci, qui a également son importance : le triangle formé entre le nombril, le point G, et l’articulation de l’épaule, est un triangle isocèle, ce qui veut dire que le point G est à égale distance du nombril et de l’articulation de l’épaule.
C’est en quelque sorte un centre secondaire, une émanation du centre principal qui et lui situé au nombril de l’homme.
Notons enfin, sur la figure ci-dessus, que le point G, qui semble – à en croire la géométrie – avoir tant d’importance pour nous faire accéder au cercle, et qui est de tant d’intérêt pour l’exécution correcte du mouvement d’Aikido, se trouve – nouvelle coïncidence – sur la barre transversale du pentagramme. Cela veut dire que l’angle de 23° dépend du pentagramme.
Cet angle, qui a donc une importance remarquable – tant pour la géométrie que pour la nature qui l’a inséré dans les proportions du corps humain et dans la trajectoire des planètes – cet angle de 23° est mesuré à partir du pentagramme.
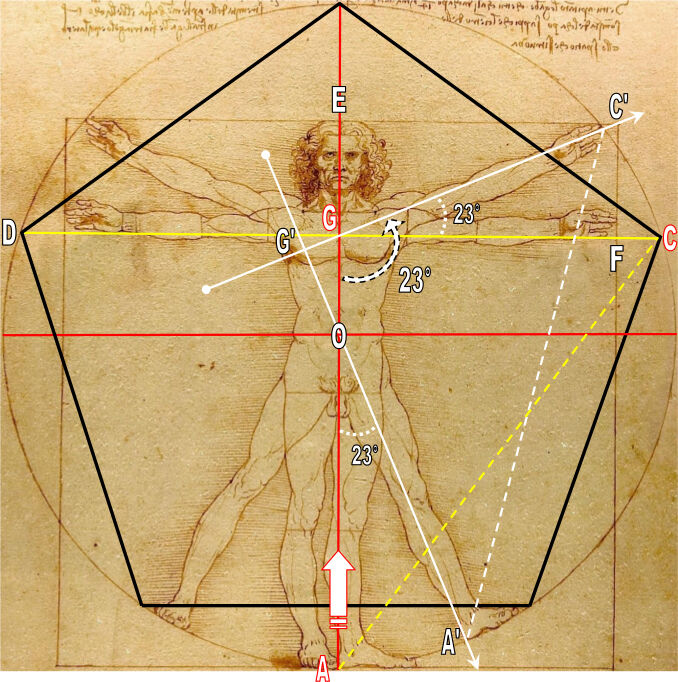
Or il existe, entre le pentagramme réguliers inscrit et la division du cercle par l’angle de 60°, un rapport géométrique curieux, outre l’intersection au point des épaules.
En effet, l’intersection entre les deux diamètres rouges à 30° et la base du pentagramme, définit deux angles (abc et ab’c’) qui sont mesurés chacun à... 23°.
Le triangle équilatéral formant la base du mouvement de l’homme en croix à 60°, est donc uni de manière géométrique, par l’angle de 23°, au pentagramme régulier :
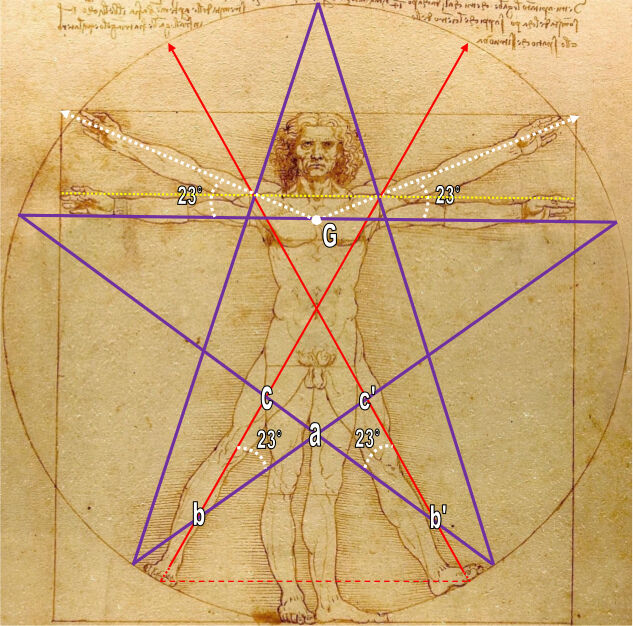
Nous ne pouvons plus avancer davantage dans cette direction de recherche, qui nous éloignerait, dans l’immédiat du moins, de l’Aikido.
Concluons donc en disant que l’homme de Vitruve nous a permis de mettre en évidence le rapport géométrique qui existe entre les pieds et les épaules de l’homme.
HV #6 nous permettra peut-être d’établir une relation entre cette découverte et l’ouverture de l’espace dans les six directions.
Philippe Voarino, octobre 2013